3.5 Vybrané speciální integrály
Teorii naleznete v kapitole 6.4 Multimediální encyklopedie nebo v kapitole 3.4 Breviáře
Příklad 1
Vypočítejte
Řešení
Zvolíme substituci 
= t
x = ln t
dx = 
Můžeme tedy psát:
= 
= 
Substituční metodou se nám tedy podařilo převézt zadaný integrál na integraci racionální lomené funkce. Nyn9 je postup obdobný jako v kapitole 3.4.
Integrand můžeme rozložit na parciální zlomky, protože kvadratický trojčlen ve jmenovateli integrandu má kladný determinant.
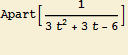
Můžeme tedy psát:
= 
=
-
Integrály vyřešíme zvlášť opět substituční metodou:
= 
= 
= 
ln s = 
ln (-1 + t)
-
= 
= 
= - 
ln u = - 
ln (2 + t)
a odtud 
= 
ln (-1 + t) - 
ln (2 + t)
Nyní jen dosadíme do substitucí:
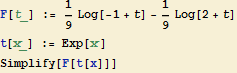
Tento integrál Mathematica neumí vypočítat přímo,
můžeme tedy pouze provézt zkoušku. Zderivujeme-li námi vypočtenou primitivní funkci, obdržíme integrand ze zadání příkladu. Počítali jsme tedy správně.
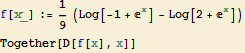
Příklad 2
Vypočítejte 
Řešení
Vhodnou substitucí převedeme integrand na racionální lomenou funkci:
ln x = t
= dt
dx = x dt
Můžeme tedy psát 
= 
Obdrželi jsme integrál z racionální lomené funkce. Stupeň polynomu v čitateli je vyšší než stupeň polynomu ve jmenovateli. Je tedy nutno vydělit čitatel jmenovatelem, zbytek potom rozložit na parciální zlomky. To vše za nás udělá příkaz Apart.
Můžeme tedy psát 
=
=-
+2
-
Tyto tři integrály jsou již jednoduché, i když u dvou z nich integrálů je opět nutno použít substituce (jsou stejného typu jako Příklad 1 v kapitole 3.4), my je však vypočítáme programem Mathematica
Teď ještě dosadíme zpátky první substituci 
= t.
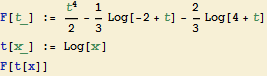
Tento integrál zvládne program Mathematica vypočítat i přímo:
